Abstract.
The
main problem is that using X-rays, we have determined the crystal
lattices of different materials, and why they are so, and not others are
not yet known. For
example, copper crystallizes in the fcc lattice, and iron in the bcc,
which becomes fcc on heating, this is used for heat treatment of steels.
Copper does not change the crystal lattice when heated.
There are many factors affecting the crystallization in the literature, so they decided to remove them as much as possible, and the metal model in the article, say so, is ideal, i.e. all atoms are the same (pure metal) without inclusions, without implants, without defects, etc. using the Hall effect and other data on properties, as well as the calculations of Ashcroft and Mermin, my main determining factor for the type of lattice was the core of the atom or ion, which resulted from the transfer of some electrons to the conduction band.
It turned out that the metal bond is due not only to the socialization of electrons, but also to external electrons of atomic cores, which determine the direction or type of the crystal lattice.
The change in the type of metal lattice can be connected with the transition of an electron to the conduction band or its return from this zone. Phase transition.
There are many factors affecting the crystallization in the literature, so they decided to remove them as much as possible, and the metal model in the article, say so, is ideal, i.e. all atoms are the same (pure metal) without inclusions, without implants, without defects, etc. using the Hall effect and other data on properties, as well as the calculations of Ashcroft and Mermin, my main determining factor for the type of lattice was the core of the atom or ion, which resulted from the transfer of some electrons to the conduction band.
It turned out that the metal bond is due not only to the socialization of electrons, but also to external electrons of atomic cores, which determine the direction or type of the crystal lattice.
The change in the type of metal lattice can be connected with the transition of an electron to the conduction band or its return from this zone. Phase transition.
It
is shown that in the general case, the metal bond in the closest
packages (hec and fcc) between the centrally chosen atom and its
neighbors is presumably carried out by means of nine (9) directional
bonds, in contrast to the number of neighbors equal to 12 (twelve)
(coordination number) .
Probably the "alien" 3 (three) atoms are present in the coordination number 12 stereometrically, and not because of the connection. The answer is to give an experimental test.
Probably the "alien" 3 (three) atoms are present in the coordination number 12 stereometrically, and not because of the connection. The answer is to give an experimental test.
Introduction
While it is not possible in general to derive from the quantum mechanical calculations the crystal structure of the metal over the electronic structure of the atom, although, for example, Gantshorn and Delinger pointed out a possible relationship between the presence of a cubic body-centered lattice in the subgroups of titanium, vanadium, chromium and the presence of valence d - orbitals. It is easy to see that four hybrid orbitals are directed along four solid cube diagonals and are well suited for coupling each atom to its 8 neighbors in a cubic body-centered lattice. In this case, the remaining orbitals are directed to the centers of the faces of the unit cell and, possibly, can participate in the connection of the atom with its six second neighbors / 3 /.
The first coordination number (K.Ch.1) "8" plus the second coordination number (K.C.2) "6" is equal to "14".
In simple examples, we show that one bond for a diamond at a packing density of 34% and a coordination number of 4 is 34%: 4 = 8.5%.
In a cubic primitive lattice, the packing density is 52% and the coordination number 6 is 52%: b = 8.66%.
In a cubic body-centered lattice, the packing density of 68% and the coordination number 8 are 68%: 8 = 8.5%.
In a face-centered cubic lattice, the packing density is 74% and the coordination number 12 is 74%: 12 = 6.16%, and if 74%: 9 = 8.22%.
In a hexagonal lattice, the packing density is 74% and the coordination number 12 is 74%: 12 = 6.16%, and if 74%: 9 = 8.22%.
Obviously, these 8.66-8.22% carry a certain physical meaning. The remaining 26% is a multiple of 8.66 and 100% hypothetical packing density is possible with 12 links. But is this possibility real?
The outer electrons of the last shell or subshells of the metal atom form a conduction band. The number of electrons in the conduction band affects the Hall constant, the coefficient of all-round compression, and so on.
Let us construct the model of the metal element so that the remaining electrons, after filling the conduction band, the external electrons of the last shell or subshells of the atomic core somehow influenced the structure of the crystal structure (for example: for bcc lattice-8 valence electrons, and for HEC and FCC -12 or 9).
Obviously, to confirm our model it is necessary to compare the experimental and theoretical data on Hall, the coefficient of all-round compression, and so on.
While it is not possible in general to derive from the quantum mechanical calculations the crystal structure of the metal over the electronic structure of the atom, although, for example, Gantshorn and Delinger pointed out a possible relationship between the presence of a cubic body-centered lattice in the subgroups of titanium, vanadium, chromium and the presence of valence d - orbitals. It is easy to see that four hybrid orbitals are directed along four solid cube diagonals and are well suited for coupling each atom to its 8 neighbors in a cubic body-centered lattice. In this case, the remaining orbitals are directed to the centers of the faces of the unit cell and, possibly, can participate in the connection of the atom with its six second neighbors / 3 /.
The first coordination number (K.Ch.1) "8" plus the second coordination number (K.C.2) "6" is equal to "14".
In simple examples, we show that one bond for a diamond at a packing density of 34% and a coordination number of 4 is 34%: 4 = 8.5%.
In a cubic primitive lattice, the packing density is 52% and the coordination number 6 is 52%: b = 8.66%.
In a cubic body-centered lattice, the packing density of 68% and the coordination number 8 are 68%: 8 = 8.5%.
In a face-centered cubic lattice, the packing density is 74% and the coordination number 12 is 74%: 12 = 6.16%, and if 74%: 9 = 8.22%.
In a hexagonal lattice, the packing density is 74% and the coordination number 12 is 74%: 12 = 6.16%, and if 74%: 9 = 8.22%.
Obviously, these 8.66-8.22% carry a certain physical meaning. The remaining 26% is a multiple of 8.66 and 100% hypothetical packing density is possible with 12 links. But is this possibility real?
The outer electrons of the last shell or subshells of the metal atom form a conduction band. The number of electrons in the conduction band affects the Hall constant, the coefficient of all-round compression, and so on.
Let us construct the model of the metal element so that the remaining electrons, after filling the conduction band, the external electrons of the last shell or subshells of the atomic core somehow influenced the structure of the crystal structure (for example: for bcc lattice-8 valence electrons, and for HEC and FCC -12 or 9).
Obviously, to confirm our model it is necessary to compare the experimental and theoretical data on Hall, the coefficient of all-round compression, and so on.
GROSS, QUALITATIVE DETERMINATION OF QUANTITY
ELECTRONS IN THE CONDUCTIVITY METAL - ELEMENT.
EXPLANATION OF FACTORS INFLUENCING THE EDUCATION OF TYPE
GRANTS OF THE MONOCRYSTAL AND ON THE SIGN OF THE CONSTANT HALL.
(Algorithm for constructing a model)
ELECTRONS IN THE CONDUCTIVITY METAL - ELEMENT.
EXPLANATION OF FACTORS INFLUENCING THE EDUCATION OF TYPE
GRANTS OF THE MONOCRYSTAL AND ON THE SIGN OF THE CONSTANT HALL.
(Algorithm for constructing a model)
Let us try to relate the external electrons of the atom of a given
element to the structure of its crystal lattice, taking into account the
need for directed bonds (chemistry) and the presence of socialized
electrons (physics) responsible for galvanomagnetic properties.
Measurements of the Hall field make it possible to determine the sign of the charge carriers in the conduction band. One
of the remarkable features of the Hall effect is, however, that in some
metals the Hall coefficient is positive, and therefore the carriers in
them must apparently have a charge opposite to the electron charge / 1
/. At
room temperature, this refers to the following metals: vanadium,
chromium, manganese, iron, cobalt, zinc, zirconium, niobium, molybdenum,
ruthenium, rhodium, cadmium, cerium, praseodymium, neodymium,
ytterbium, hafnium, tantalum, tungsten, rhenium, iridium , thallium, lead / 2 /. The solution of this puzzle should be given by a complete quantum mechanical theory of a solid.
Approximately, as for some cases of application of the Born-Karman boundary conditions, we consider a strongly simplified one-dimensional case of the conduction band. Option one: a thin closed tube, completely filled with electrons except one. The diameter of the electron is approximately equal to the diameter of the tube. With such a filling of the zone, with the local movement of the electron, there is an opposite movement of the "place" of the non-filled tube, the electron, that is, the motion of a non-negative charge. Option two: in the tube of one electron - it is possible to move only one charge - a negatively charged electron. From these two extreme variants it is seen that the sign of carriers, determined from the Hall coefficient, to some extent, should depend on the filling of the conduction band by electrons.
Picture 1.
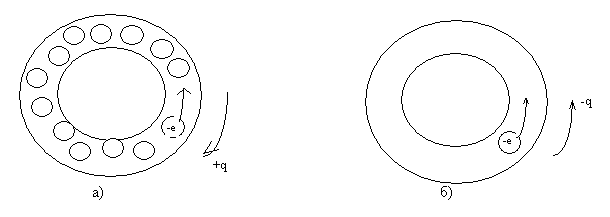
Fig. 1. Schematic representation of the conduction band of two different metals (Scales not observed).
a) - the first option;
b) the second option.
Approximately, as for some cases of application of the Born-Karman boundary conditions, we consider a strongly simplified one-dimensional case of the conduction band. Option one: a thin closed tube, completely filled with electrons except one. The diameter of the electron is approximately equal to the diameter of the tube. With such a filling of the zone, with the local movement of the electron, there is an opposite movement of the "place" of the non-filled tube, the electron, that is, the motion of a non-negative charge. Option two: in the tube of one electron - it is possible to move only one charge - a negatively charged electron. From these two extreme variants it is seen that the sign of carriers, determined from the Hall coefficient, to some extent, should depend on the filling of the conduction band by electrons.
Picture 1.

Fig. 1. Schematic representation of the conduction band of two different metals (Scales not observed).
a) - the first option;
b) the second option.
The motion of the electrons will also be imposed by an order of magnitude on the structure of the conduction band, temperature, impurities, and defects, and magnons for magnetic materials and scattering by magnetic quasiparticles.
In the table below it is not difficult to see that almost all the superconductor metals in the conduction band contain two or more electrons from the atom. They are metals: zirconium, zinc, tungsten, vanadium, thallium, titanium, tantalum, ruthenium, rhenium, lead, osmium, niobium, lanthanum, iridium, hafnium, cadmium, aluminum.
Since our arguments are crude, we take into account in the sequel so far only the filling of the conduction band by electrons. We fill the conduction band with electrons so that the outer electrons of the atomic cores exert influence on the formation of the type of crystallization lattice. Suppose that the number of external electrons on the last shell of the atomic core, after filling the conduction band, is equal to the number of neighbors atoms (coordination number) / 5 /. Coordination numbers of HEC, fcc (hexagonal and face-centered) densest packages 12 and 18, and body-centered lattice (bcc) 8 and 14/3 /.
Let's construct the table taking into account the above. The room temperature.
Element RH 1010 (m3 / K) Z. (pcs.) Z frame (pcs.) Grid type
The below table is filled in compliance with the above judgements.
| Element | RH . 1010 (м3/K) | Z. (number) | Z kernel (number) | Lattice type |
| Na | -2,30 | 1 | 8 | body-centered |
| Mg | -0,90 | 1 | 9 | volume-centered |
| Al | -0,38 | 2 | 9 | face-centered |
| Al | -0,38 | 1 | 12 | face-centered |
| K | -4,20 | 1 | 8 | body-centered |
| Ca | -1,78 | 1 | 9 | face-centered |
| Ca | T=737K | 2 | 8 | body-centered |
| Sc | -0,67 | 2 | 9 | volume-centered |
| Sc | -0,67 | 1 | 18 | volume-centered |
| Ti | -2,40 | 1 | 9 | volume-centered |
| Ti | -2,40 | 3 | 9 | volume-centered |
| Ti | T=1158K | 4 | 8 | body-centered |
| V | +0,76 | 5 | 8 | body-centered |
| Cr | +3,63 | 6 | 8 | body-centered |
| Fe | +8,00 | 8 | 8 | body-centered |
| Fe | +8,00 | 2 | 14 | body-centered |
| Fe | Т=1189K | 7 | 9 | face-centered |
| Fe | Т=1189K | 4 | 12 | face-centered |
| Co | +3,60 | 8 | 9 | volume-centered |
| Co | +3,60 | 5 | 12 | volume-centered |
| Ni | -0,60 | 1 | 9 | face-centered |
| Cu | -0,52 | 1 | 18 | face-centered |
| Cu | -0,52 | 2 | 9 | face-centered |
| Zn | +0,90 | 2 | 18 | volume-centered |
| Zn | +0,90 | 3 | 9 | volume-centered |
| Rb | -5,90 | 1 | 8 | body-centered |
| Y | -1,25 | 2 | 9 | volume-centered |
| Zr | +0,21 | 3 | 9 | volume-centered |
| Zr | Т=1135К | 4 | 8 | body-centered |
| Nb | +0,72 | 5 | 8 | body-centered |
| Mo | +1,91 | 6 | 8 | body-centered |
| Ru | +22 | 7 | 9 | volume-centered |
| Rh | +0,48 | 5 | 12 | face-centered |
| Rh | +0,48 | 8 | 9 | face-centered |
| Pd | -6,80 | 1 | 9 | face-centered |
| Ag | -0,90 | 1 | 18 | face-centered |
| Ag | -0,90 | 2 | 9 | face-centered |
| Cd | +0,67 | 2 | 18 | volume-centered |
| Cd | +0,67 | 3 | 9 | volume-centered |
| Cs | -7,80 | 1 | 8 | body-centered |
| La | -0,80 | 2 | 9 | volume-centered |
| Ce | +1,92 | 3 | 9 | face-centered |
| Ce | +1,92 | 1 | 9 | face-centered |
| Pr | +0,71 | 4 | 9 | volume-centered |
| Pr | +0,71 | 1 | 9 | volume-centered |
| Nd | +0,97 | 5 | 9 | volume-centered |
| Nd | +0,97 | 1 | 9 | volume-centered |
| Gd | -0,95 | 2 | 9 | volume-centered |
| Gd | T=1533K | 3 | 8 | body-centered |
| Tb | -4,30 | 1 | 9 | volume-centered |
| Tb | Т=1560К | 2 | 8 | body-centered |
| Dy | -2,70 | 1 | 9 | volume-centered |
| Dy | Т=1657К | 2 | 8 | body-centered |
| Er | -0,341 | 1 | 9 | volume-centered |
| Tu | -1,80 | 1 | 9 | volume-centered |
| Yb | +3,77 | 3 | 9 | face-centered |
| Yb | +3,77 | 1 | 9 | face-centered |
| Lu | -0,535 | 2 | 9 | volume-centered |
| Hf | +0,43 | 3 | 9 | volume-centered |
| Hf | Т=2050К | 4 | 8 | body-centered |
| Ta | +0,98 | 5 | 8 | body-centered |
| W | +0,856 | 6 | 8 | body-centered |
| Re | +3,15 | 6 | 9 | volume-centered |
| Os | <0 | 4 | 12 | volume-centered |
| Ir | +3,18 | 5 | 12 | face-centered |
| Pt | -0,194 | 1 | 9 | face-centered |
| Au | -0,69 | 1 | 18 | face-centered |
| Au | -0,69 | 2 | 9 | face-centered |
| Tl | +0,24 | 3 | 18 | volume-centered |
| Tl | +0,24 | 4 | 9 | volume-centered |
| Pb | +0,09 | 4 | 18 | face-centered |
| Pb | +0,09 | 5 | 9 | face-centered |
Where: RH - Hall constant (Hall coefficient)
Z is the assumed number of electrons, given by one atom to the conduction band
Z skeleton. - number of outer electrons of the atomic core on the last shell.
The lattice type is the type of crystal structure of the metal at room temperature and in some cases for phase transition temperatures (T).
Conclusions.
Despite
the crude assumptions, it can be seen from the table that the larger
the element atom gives electrons to the conduction band, the more
positive the Hall constant, and conversely the Hall constant is negative
for the elements that gave one or two electrons to the conduction band,
which does not contradict the conclusions of Peierls , as
well as the connection between the conduction electrons (Z) and valence
electrons (Zost), which cause the crystal structure.
Using
the method of counting down from the experimental values of the
coefficient of all-round compression to theoretical values using the
formulas of Ashcroft and Mermin [1], determining the number Z, one can
be sure of its close coincidence with that given in Table 1.
The metallic bond appears to be conditioned by both the socialized electrons and the "valence" electrons-the outer electrons of the atomic core.
The metallic bond appears to be conditioned by both the socialized electrons and the "valence" electrons-the outer electrons of the atomic core.
The phase transitions of an element from one lattice to another can be
explained by transferring one of the outer electrons of the atomic core
to the conduction band of the metal or by returning it from the
conduction band to the outer shell of the core under the influence of
external factors (pressure, temperature).
We tried to give a clue, but we got a new, physicochemical properties of the elements, which are pretty well explained, the riddle is a "coordination number" - 9 (nine) for HCC and HEC. Such a frequent occurrence of the number-9 in the table above suggests that the densest packages are not sufficiently investigated.
We tried to give a clue, but we got a new, physicochemical properties of the elements, which are pretty well explained, the riddle is a "coordination number" - 9 (nine) for HCC and HEC. Such a frequent occurrence of the number-9 in the table above suggests that the densest packages are not sufficiently investigated.
Appendix 1
Metal bond in the closest packages (HEC, HCC)
From the arguments about the number of directed bonds (or pseudo-connections, since there is a conduction band between the neighboring metal atoms), equal to nine in the number of outer electrons of the atomic core for the densest packages, it follows that, by analogy with the bcc lattice (eight neighbor atoms in the first coordination sphere) for HEK and fcc lattices in the first coordination sphere, there should be nine, and we have 12 atoms. But 9 atoms of neighbors bound by any centrally chosen atom are indirectly confirmed by experimental data on the Hall and the modulus of all-round compression (and in the experiments on the de Haas-van Alfene effect, the number of oscillations is a multiple of nine).
Hence, for the three atoms out of 12, we must seek differences from the remaining atoms of the coordination sphere.
From the arguments about the number of directed bonds (or pseudo-connections, since there is a conduction band between the neighboring metal atoms), equal to nine in the number of outer electrons of the atomic core for the densest packages, it follows that, by analogy with the bcc lattice (eight neighbor atoms in the first coordination sphere) for HEK and fcc lattices in the first coordination sphere, there should be nine, and we have 12 atoms. But 9 atoms of neighbors bound by any centrally chosen atom are indirectly confirmed by experimental data on the Hall and the modulus of all-round compression (and in the experiments on the de Haas-van Alfene effect, the number of oscillations is a multiple of nine).
Hence, for the three atoms out of 12, we must seek differences from the remaining atoms of the coordination sphere.
Fig.1.1, d, e shows the coordination spheres in the densest hexagonal and cubic packs.
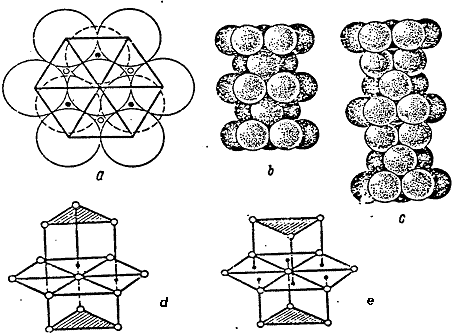
Fig.1.1. Dense Packing.
It should be noted that in the hexagonal packing, the triangles of upper and lower bases are unindirectional, whereas in the hexagonal packing they are not unindirectional.
Fig. 1.1. Tight packing
Let's pay attention, that in a hexagonal packing triangles of the top and bottom bases are turned in one and the same party, and in cubic - in different.
Literature: BF Ormont "Introduction to physical chemistry and crystal chemistry of semiconductors", Moscow, 1968
Let's pay attention, that in a hexagonal packing triangles of the top and bottom bases are turned in one and the same party, and in cubic - in different.
Literature: BF Ormont "Introduction to physical chemistry and crystal chemistry of semiconductors", Moscow, 1968
Appendix 2
Theoretical calculation of the uniform compression modulus (B).
B = (6,13/(rs/ao))5* (10)10 dyne/cm2
Where B is the uniform compression modulus ao is the Bohr radius rs - the radius of the sphere with the volume being equal to
the volume falling at one conductivity electron.
rs=(3/4p n)1/3, p=3,14
Where n is the density of conductivity electrons.
Theoretical calculation of the uniform compression modulus (B).
B = (6,13/(rs/ao))5* (10)10 dyne/cm2
Where B is the uniform compression modulus ao is the Bohr radius rs - the radius of the sphere with the volume being equal to
the volume falling at one conductivity electron.
rs=(3/4p n)1/3, p=3,14
Where n is the density of conductivity electrons.
Table 1. Calculation according to Ashcroft and Mermine Element Z rs/ao theoretical calculated
Table 2. Calculation according to the models considered in this paper
| Z | rs/a0 | B theoretical | B calculated | |
| Cs | 1 | 5.62 | 1.54 | 1.43 |
| Cu | 1 | 2.67 | 63.8 | 134.3 |
| Ag | 1 | 3.02 | 34.5 | 99.9 |
| Al | 3 | 2.07 | 228 | 76.0 |
| Z | rs/a0 | B theoretical | B calculated | |
| Cs | 1 | 5.62 | 1.54 | 1.43 |
| Cu | 2 | 2.12 | 202.3 | 134.3 |
| Ag | 2 | 2.39 | 111.0 | 99.9 |
| Al | 2 | 2.40 | 108.6 | 76.0 |
According
to / 1 /, the number of Z-electrons in the conduction band was obtained
by the authors, presumably based on the valency of the metal over
oxygen and hydrogen, and must be questioned, since the experimental data on Hall and the modulus of all-round compression are close to theoretical only for alkali metals. Bcc grating.
Of
course, the pressure of free-electron gases alone does not completely
determine the resistance of the metal to compression, nevertheless in
the second case of calculation the theoretical modulus of all-round
compression lies closer to the experimental one, on the one hand. Obviously,
it is necessary to take into account the second factor-the effect on
the module of the "valence" or outer electrons of the atomic core, which
determine the crystal lattice.
While still studying at the institute, I tried to explain the phase transitions in barium titanate. Since then I have been working on the nature of crystal lattices and different properties of chemical elements. It
turned out that when heated, the crystal lattices of lithium and
beryllium behave approximately like scandium and titanium lattices.
Therefore I doubted the absolute correctness of the table of elements and developed amendments.
Therefore I doubted the absolute correctness of the table of elements and developed amendments.
This article sets out the views on the classification of all known
chemical elements, those fundamental components of which the Earth and
the entire Universe consists.
The innovation of this work is that in the table of elements constructed according to the Mendeleyev’s law and Van-den- Broek’s rule, new chemical elements with atomic numbers 72-75 and 108-111 are supposedly revealed, and also it is shown that for heavy elements starting with hafnium, the nuclei of atoms contain a larger number of protons than is generally accepted. Perhaps the mathematical apparatus of quantum mechanics missed some solutions because the atomic nucleus in calculations is taken as a point.
All cells in the table are full. If this table takes place, I would like to name groups of elements with the numbers 72-75 and 108-111, the islets of Filipenka Henadzi.
The rule of van den Broeck, a lover of nuclear physics, turned out to be more general than Mendeleyev's periodicity and calculations of quantum mechanics. The table must be filled in all cells according to the law or rule, and if somebody does not fill in, there should be an explanation of this by this law or rule. Therefore, the cells of the physical table were filled in both at http://tableelements.blogspot.com and unknown items with numbers 72-75 and 108-111 appeared. Which required explanation. When considering the results of measuring the charges of nuclei or atomic numbers by James Chadwick, I noticed that the charge of the core of platinum is rather equal not to 78, but to 82, which corresponds to the developed table. For almost 30 years I have raised the question of the repetition of measurements of the charges of atomic nuclei, since uranium is probably more charged than accepted, and it is used at nuclear power plants.

The innovation of this work is that in the table of elements constructed according to the Mendeleyev’s law and Van-den- Broek’s rule, new chemical elements with atomic numbers 72-75 and 108-111 are supposedly revealed, and also it is shown that for heavy elements starting with hafnium, the nuclei of atoms contain a larger number of protons than is generally accepted. Perhaps the mathematical apparatus of quantum mechanics missed some solutions because the atomic nucleus in calculations is taken as a point.
All cells in the table are full. If this table takes place, I would like to name groups of elements with the numbers 72-75 and 108-111, the islets of Filipenka Henadzi.
The rule of van den Broeck, a lover of nuclear physics, turned out to be more general than Mendeleyev's periodicity and calculations of quantum mechanics. The table must be filled in all cells according to the law or rule, and if somebody does not fill in, there should be an explanation of this by this law or rule. Therefore, the cells of the physical table were filled in both at http://tableelements.blogspot.com and unknown items with numbers 72-75 and 108-111 appeared. Which required explanation. When considering the results of measuring the charges of nuclei or atomic numbers by James Chadwick, I noticed that the charge of the core of platinum is rather equal not to 78, but to 82, which corresponds to the developed table. For almost 30 years I have raised the question of the repetition of measurements of the charges of atomic nuclei, since uranium is probably more charged than accepted, and it is used at nuclear power plants.
таблица элементов
| H 1 | He 2 | Li 3 | Be 4 | B 5 | C 6 | N 7 | O 8 | F 9 | Ne 10 | Na 11 | Mg 12 | Al 13 | Si 14 | P1 5 | S 16 | Cl 17 | A 1 | |
| K 19 | Ca 20 | Sc 21 | Ti 22 | V 23 | Cr 24 | Mn 25 | Fe 26 | Co 27 | Ni 28 | Cu 29 | Zn 30 | Ga 31 | Ge 32 | As 33 | Se 34 | Br 35 | Kr 36 | |
| Rb 37 | Sr 38 | Y 39 | Zr 40 | Nb 41 | Mo 42 | Tc 43 | Ru 44 | Rh 45 | Pd 46 | Ag 47 | Cd 48 | In 49 | Sn 50 | Sb 51 | Te 52 | I 53 | Xe 54 | |
| Cs 55 | Ba 56 | La 57 | Ce 58 | Pr 59 | Nd 60 | Pm 61 | Sm 62 | Eu 63 | Gd 64 | Tb 65 | Dy 66 | Ho 67 | Er 68 | Tu 69 | Yb 70 | Lu 71 | ? 72 | |
| ? 73 | ? 74 | ? 75 | Hf 76 | Ta 77 | W 78 | Re 79 | Os 80 | Ir 81 | Pt 82 | Au 83 | Hg 84 | Tl 85 | Pb 86 | Bi 87 | Po 88 | At 89 | Rn 90 | |
| Fr 91 | Ra 92 | Ac 93 | Th 94 | Pa 95 | U 96 | Np 97 | Pu 98 | Am 99 | Cm 100 | Bk 101 | Cf 102 | Es 103 | Fm 104 | Md 105 | No 106 | Lr 107 | ||
"Our philosophy that it is impossible to describe nature mathematically by one hundred percent was confirmed. But it strives, of course, to such a description is necessary."
Henadzi Filipenka
Henadzi Filipenka
Each subsequent chemical element is different
from the previous one in that in its core the number of protons
increases by one, and the number of neutrons increases, in
in general, several. In the literature this strange
ratio of the number of neutrons to the number of protons for any
the kernel is not explained. The article proposes a model nucleus,
explaining this phenomenon.
from the previous one in that in its core the number of protons
increases by one, and the number of neutrons increases, in
in general, several. In the literature this strange
ratio of the number of neutrons to the number of protons for any
the kernel is not explained. The article proposes a model nucleus,
explaining this phenomenon.
For the construction of the atomic nucleus model, we note that with alpha-
radioactivity of the helium nucleus is approximately equal to the energy.
Therefore, on the outer layer of the core shell, we place all the protons with such
the same number of neutrons. At the same time, on one energy
Only bosons can be in the
outer shell of the alpha-particle nucleus and are. Inside the Kernel
We will arrange the remaining neutrons, whose task will be
weakening of electrostatic fields of repulsion of protons.
Assuming the core to be spherical, and the radii of the proton and neutron
approximately the same, for any element we get the kernel model,
explaining the ratio of the number of neutrons to the number of protons,
which follows from the packing of the nucleus of the atom by nucleons. Low accuracy for light elements.
radioactivity of the helium nucleus is approximately equal to the energy.
Therefore, on the outer layer of the core shell, we place all the protons with such
the same number of neutrons. At the same time, on one energy
Only bosons can be in the
outer shell of the alpha-particle nucleus and are. Inside the Kernel
We will arrange the remaining neutrons, whose task will be
weakening of electrostatic fields of repulsion of protons.
Assuming the core to be spherical, and the radii of the proton and neutron
approximately the same, for any element we get the kernel model,
explaining the ratio of the number of neutrons to the number of protons,
which follows from the packing of the nucleus of the atom by nucleons. Low accuracy for light elements.
We
construct the table so that to observe the law of Mendeleyev
periodicity, the VanDen-Brook rule and to fill all the cells of the
table. In
quantum mechanics, by default, in each successive element, the charge
of the nucleus increases at its center by one, and the electrons fill
with spdf configurations. Our
nuclear charge is located on the surface, since the number of protons
and the number of neutrons in the nucleus are such that protons and
neutrons should be in the outer layer of the nucleus, and only neutrons
inside, that is, a shell forms on the surface of the nucleus. In addition, protons must be repelled, and also attracted by an electronic fur coat. The question is whether the kernel can be considered a point in the calculations and up to what times? And the question is whether and when the proton will be inside the nucleus. There is also an apparatus of quantum mechanics, which confirmed the law of Mendeleyev. In his calculations, the nucleus and electrons are taken as points.
But if a proton gets into the nucleus for some reason, then the corresponding electron will be on the very "low" orbit. Quantum mechanics still does not notice such electrons. Or in other words, in elements 72-75 and 108-111, some protons begin to be placed inside the nucleus and the charge of the nucleus is screened, in calculations it can not be taken as a point.
I understood this when I thought of Chadwick's experiments on the determination of nuclear charges in particular platinum. If we plot the results from copper through silver to platinum, we see a clear trend on the charge of platinum not 78, but more. I have 82.
This is the correct and real table, not the pieces. Beginning with Hafnium, the number of protons and, correspondingly, neutrons in the nuclei of the elements changes in comparison with what is generally accepted today.
But if a proton gets into the nucleus for some reason, then the corresponding electron will be on the very "low" orbit. Quantum mechanics still does not notice such electrons. Or in other words, in elements 72-75 and 108-111, some protons begin to be placed inside the nucleus and the charge of the nucleus is screened, in calculations it can not be taken as a point.
I understood this when I thought of Chadwick's experiments on the determination of nuclear charges in particular platinum. If we plot the results from copper through silver to platinum, we see a clear trend on the charge of platinum not 78, but more. I have 82.
This is the correct and real table, not the pieces. Beginning with Hafnium, the number of protons and, correspondingly, neutrons in the nuclei of the elements changes in comparison with what is generally accepted today.
Literature:
1) Solid state physics. N.W. Ashcroft, N.D. Mermin. Cornell University, 1975
2) Characteristics of elements. G.V. Samsonov. Moscow, 1976
3) Grundzuge der Anorganischen Kristallchemie. Von. Dr. Heinz Krebs. Universitat Stuttgart, 1968
4) Physics of metals. Y.G. Dorfman, I.K. Kikoin. Leningrad, 1933
5) What affects crystals characteristics. G.G.Skidelsky. Engineer N 8, 1989
1) Solid state physics. N.W. Ashcroft, N.D. Mermin. Cornell University, 1975
2) Characteristics of elements. G.V. Samsonov. Moscow, 1976
3) Grundzuge der Anorganischen Kristallchemie. Von. Dr. Heinz Krebs. Universitat Stuttgart, 1968
4) Physics of metals. Y.G. Dorfman, I.K. Kikoin. Leningrad, 1933
5) What affects crystals characteristics. G.G.Skidelsky. Engineer N 8, 1989
6. Г. Г. Филипенко. «Подозрительные» области в
периодической системе, "Техника и наука", №4,
Москва, 1990.
7. Г. Г. Филипенко. Предлагается модель ядра атома,
"Инженер", №4, Москва, 1991.
периодической системе, "Техника и наука", №4,
Москва, 1990.
7. Г. Г. Филипенко. Предлагается модель ядра атома,
"Инженер", №4, Москва, 1991.
https://fhenadzi.wordpress.com


